Abstract
-
Background
- Hydrocephalus (HCP) is one of the most significant concerns in neurosurgical patients because it can cause increased intracranial pressure (ICP), resulting in mortality and morbidity. To date, machine learning (ML) has been helpful in predicting continuous outcomes. The primary objective of the present study was to identify the factors correlated with ICP, while the secondary objective was to compare the predictive performances among linear, non-linear, and ML regression models for ICP prediction.
-
Methods
- A total of 412 patients with various types of HCP who had undergone ventriculostomy was retrospectively included in the present study, and intraoperative ICP was recorded following ventricular catheter insertion. Several clinical factors and imaging parameters were analyzed for the relationship with ICP by linear correlation. The predictive performance of ICP was compared among linear, non-linear, and ML regression models.
-
Results
- Optic nerve sheath diameter (ONSD) had a moderately positive correlation with ICP (r=0.530, P<0.001), while several ventricular indexes were not statistically significant in correlation with ICP. For prediction of ICP, random forest (RF) and extreme gradient boosting (XGBoost) algorithms had low mean absolute error and root mean square error values and high R2 values compared to linear and non-linear regression when the predictive model included ONSD and ventricular indexes.
-
Conclusions
- The XGBoost and RF algorithms are advantageous for predicting preoperative ICP and establishing prognoses for HCP patients. Furthermore, ML-based prediction could be used as a non-invasive method.
-
Keywords: hydrocephalus; intracranial pressure; linear regression; machine learning; prediction
INTRODUCTION
Hydrocephalus (HCP) is one of the major problems faced by neurosurgeons because not treating or delaying treatment for HCP can cause increased intracranial pressure (ICP) and brainstem injury, leading to mortality and disability [1,2]. Elevated ICP is associated with unfavorable outcomes and poor prognoses in neurosurgical patients [3,4]. Therefore, predicting ICP before cerebrospinal fluid diversion is important to evaluate patients’ prognoses and provide advice to their relatives.
Prior studies have examined the relationships between ICP and various imaging parameters, such as optic nerve sheath diameter (ONSD) and ventricular indexes, for ICP prediction by traditional statistical analysis; however, their results have been inconclusive [5-9]. Lee et al. [5] studied HCP in adult patients and found that ONSD was significantly and linearly correlated with ICP (r=0.543, P<0.001), while Kavi et al. [6] found no correlation between ONSD and ICP using the linear correlation test. Additionally, Jenjitranant et al. [7] found that ONSD factors were significantly associated with increased ICP by logistic regression analysis.
Ventricular indexes composed of the Evans index, third ventricular index, cella media index, and ventricular score have been studied for ICP-level association [8,9]. Kim et al. [8] studied patients with communicating, non-communicating, or normal pressure HCP and found that the third ventricular index had a negative correlation with ICP (r=−0.395, P<0.01) in non-communicating HCP, while Eide et al. identified a non-significant relationship between ventricular indexes and ICP [9].
Machine learning (ML) has been used to predict various clinical outcomes in various neurosurgical fields. Further, ML classification has been commonly used in studies to predict binary classifiers and categorical outcomes [10-13]. Miyagawa et al. [11] used ML classification to predict the suspected increase of ICP in children with HCP and reported an accuracy of 91%–94%, while Schweingruber et al. [12] predicted increased ICP in patients by recurrent ML classification and reported an accuracy of 0.686–0.931. According to our literature review, however, few studies have mentioned ML regression for ICP prediction, which could be a non-invasive approach in real-world practice. Based on this gap in knowledge, the primary purpose of the present study was to identify the factors correlated with ICP, and the secondary objective was to compare predictive performances among linear, non-linear, and ML regression models for ICP prediction.
MATERIALS AND METHODS
Study Design and Population
After gaining approval from the Ethics Committee and Institutional Review Board of the Faculty of Medicine at Prince of Songkla University (REC.65-249-10-1). Informed consent from the patients was not necessary for the present study, as it involved a retrospective analysis. However, patient identification numbers were encoded before analysis. Our retrospective cohort investigation began with a review of the electronic medical records of HCP patients who were admitted and underwent ventriculostomy at a tertiary hospital between January 2014 and June 2022. Clinical characteristics and imaging parameters were collected. Patients who did not undergo preoperative cranial computed tomography (CT) imaging or who had missing data on intraoperative ICP after ventriculostomy were excluded, as shown in Figure 1.
Operational Definition
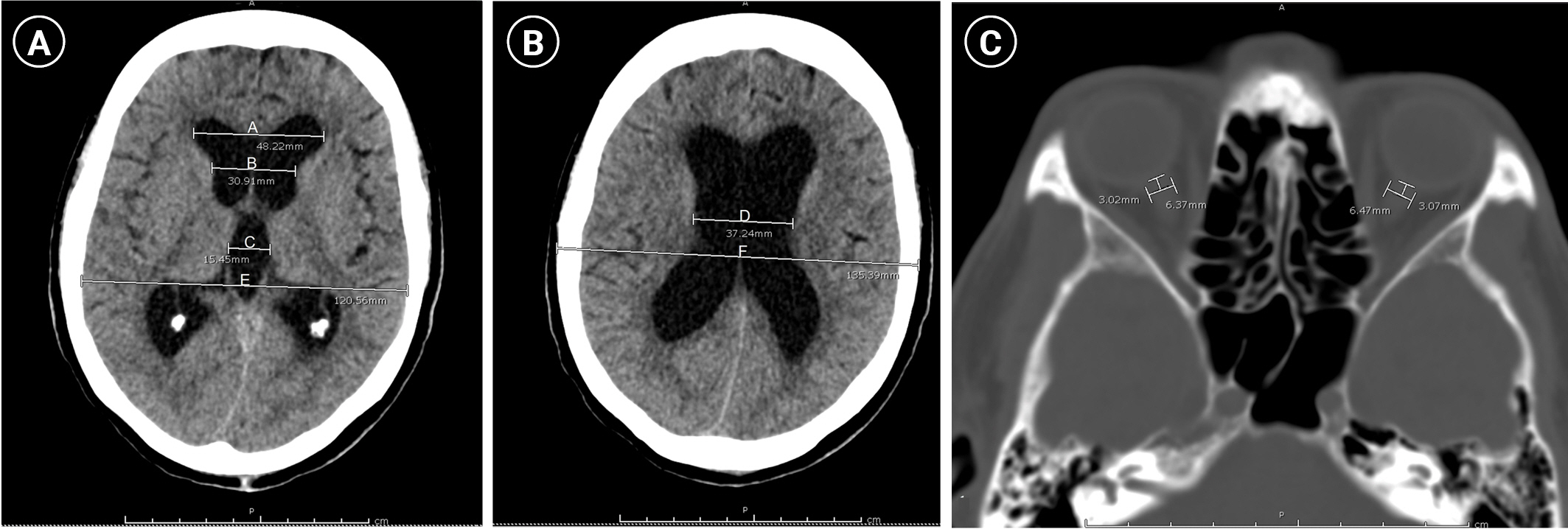
ICP was the outcome of the present study and was intraoperatively measured after ventricular catheter insertion. Therefore, ICP in cm H2O was converted to mm Hg using the equation 1 cm H2O=0.736 mm Hg [13]. Several preoperative imaging parameters were also collected for hypothesis testing. According to a study by Mataró et al. [14], several ventricular lines were estimated for calculating the ventricular indexes, as shown in Figure 2A and B. In detail, the following various lines were measured from a cranial CT scan at the level of the third ventricle: the maximum bifrontal distance of the lateral ventricle (A), the distance between the caudate nuclei at the level of the foramen of Monro (B), the maximum width of the third ventricle (C), and the maximum inner diameter of the skull at the level of the maximum bifrontal distance measurement (E). Meanwhile, the minimum width of the cella media (D) and the maximal outer interparietal diameter (F) were measured at the level of the cella media. Subsequently, the ventricular indexes were calculated as follows:
Evans index (A/E), third ventricle index (C/E), cella media index (D/F), and ventricular score [(A+B+C+D)/E×100].
The ONSD of both eyes was measured on an axis perpendicular to the optic nerve (transverse plane) at 3 mm behind the globe by axial CT imaging according to the method of Jenjitranant et al. [7], as shown in Figure 2C. Therefore, the average ONSD was calculated for analysis.
Statistical Analysis
Using descriptive statistics, the baseline characteristics of the current cohort were outlined. In detail, the categorical variables are presented as percentage, whereas the continuous variables are presented as mean and standard deviation (SD). Pearson’s correlation was used to evaluate the strength of the association; values indicating a very weak correlation ranged from 0–0.19, those indicating a weak correlation ranged from 0.2–0.39, those indicating a moderate correlation ranged from 0.4–0.59, those indicating a strong correlation ranged from 0.6–0.79, and those indicating a very strong correlation ranged from 0.8–1.0 [15]. Moreover, the correlation matrix was used for visualization with the scatterplot among various variables.
The correlation coefficient formula was used to determine the sample size for hypothesis testing [16]. In a previous study [8], a correlation coefficient of 0.543, alpha value of 0.05, and beta value of 0.1 were employed for estimation. As a result, a sample size of at least 32 patients was required for validation.
ML Regression
A random 80:20 split was used to divide the whole set of data into a training dataset and a testing dataset, respectively. Of these, the training dataset was used to construct the predictive model, while the performance of ICP prediction was estimated using the testing dataset. Various traditional regression models were performed, including linear regression, polynomial regression, log transformation, and cubic spline regression, for ICP prediction. Additionally, the following algorithms of ML regression were used to develop the models: k-nearest neighbors, decision tree, random forest (RF), extreme gradient boosting (XGBoost), and artificial neural network. In detail, 10-fold cross-validation was performed for training, and the best tuning parameters for the model of each algorithm were optimized by minimizing the root mean square error (RMSE) according to the method of Kassambara [17].
The setting of the RF in the present study was 500 trees contained in the forest and 5 nodes of the terminal node size, whereas the architecture of the artificial neural network included 2 hidden layers with 3 and 2 neurons, respectively, and a single output.
Predictive Performance Metrics
The predictive performances of the linear, non-linear, and ML models were compared using the mean absolute error (MAE), RMSE, and R2. The best model should have the highest R2 and lowest errors. Therefore, the linear, non-linear, and ML regression models were performed using the “caret” package in R version 4.0.3 (R Foundation for Statistical Computing). In addition, the ML models were provided as web application by the shiny R package.
RESULTS
Four hundred twelve patients were included in the analysis. The baseline clinical characteristics are shown in Table 1. The mean age of patients was 51 years (SD, 24 years), and more than half were female. Additionally, emergency ventriculostomy was performed in 94.2%, and two-thirds of HCP cases were obstructive cases. Intraoperative ICP was recorded in the operative notes when a ventricular catheter was inserted. The mean ICP was 31.43 mm Hg (SD, 9.45 mm Hg), and 59.2% of patients had a Glasgow coma scale score less than 9 points.
The average imaging parameters are shown in Table 2. The mean ONSD was 5.5 mm (SD, 0. 8 mm), while the mean Evans index, mean third ventricular index, mean cella media index, and mean ventricular score were 0.3 (SD, 0.1), 0.1 (SD, 0.0), 0.3 (SD, 0.1), and 95.3 (SD, 23.7), respectively.
Factors Correlated with ICP
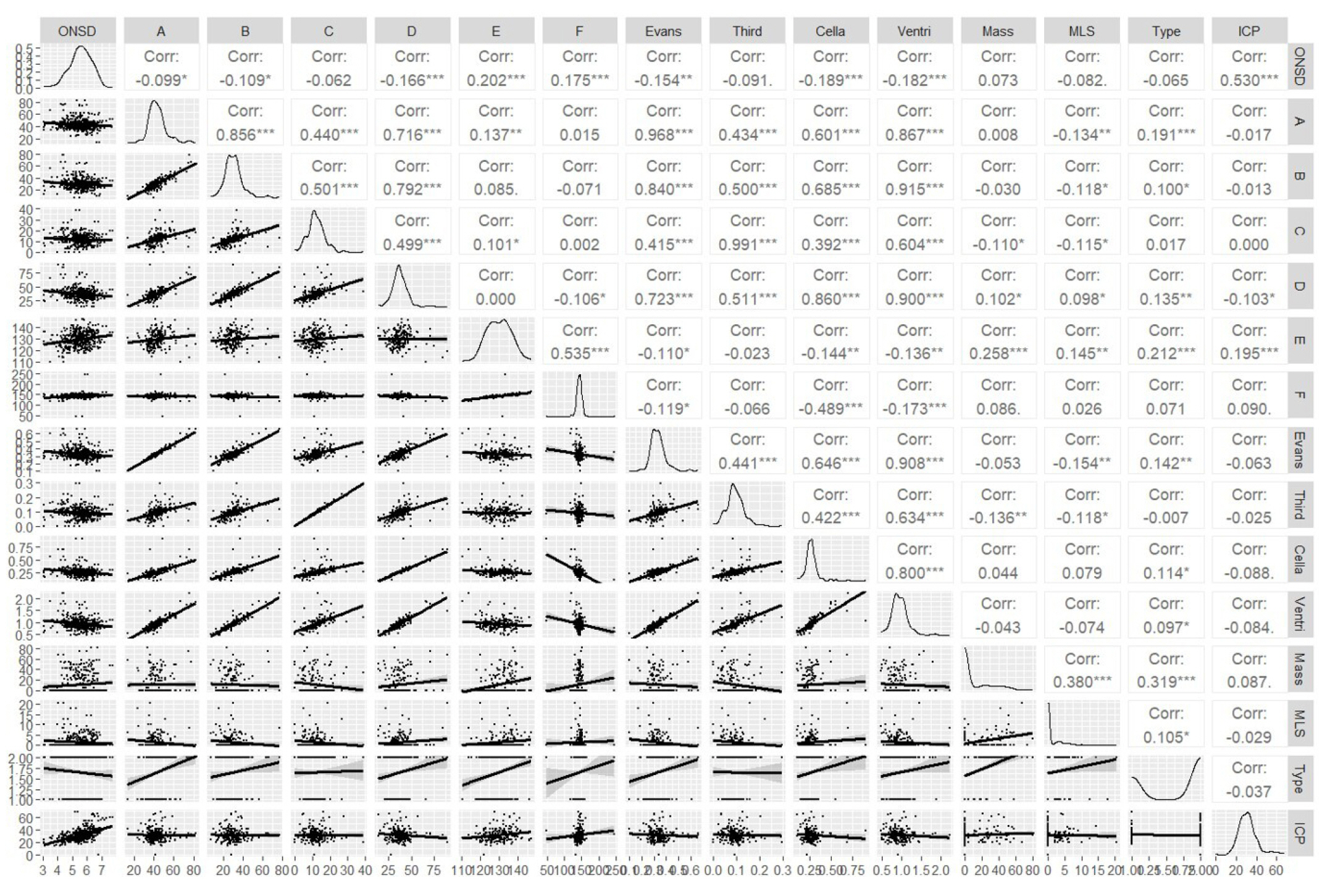
The correlations between various parameters and ICP are demonstrated in Figure 3 using a correlation matrix. The ONSD had a moderately positive correlation with ICP (r=0.530, P<0.001) according to Pearson’s correlation, whereas no ventricular indexes were statistically correlated.
Comparison of the Predictive Performance Metrics among Regression Models
After the 80:20 data split, 330 HCP patients were used to train the predictive model, while the remaining patients were used for testing performances. Although ONSD was a significant parameter related to ICP, ventricular indexes and other features were still necessary to build a predictive model and test their performances. Therefore, the following three strategies were adopted for model development and predictive performance evaluation: (1) ONSD; (2) ONSD with ventricular indexes; and (3) ONSD, ventricular indexes, and other features (mass diameters and midline shift). The predictive performances of various models for ICP are shown in Table 3.
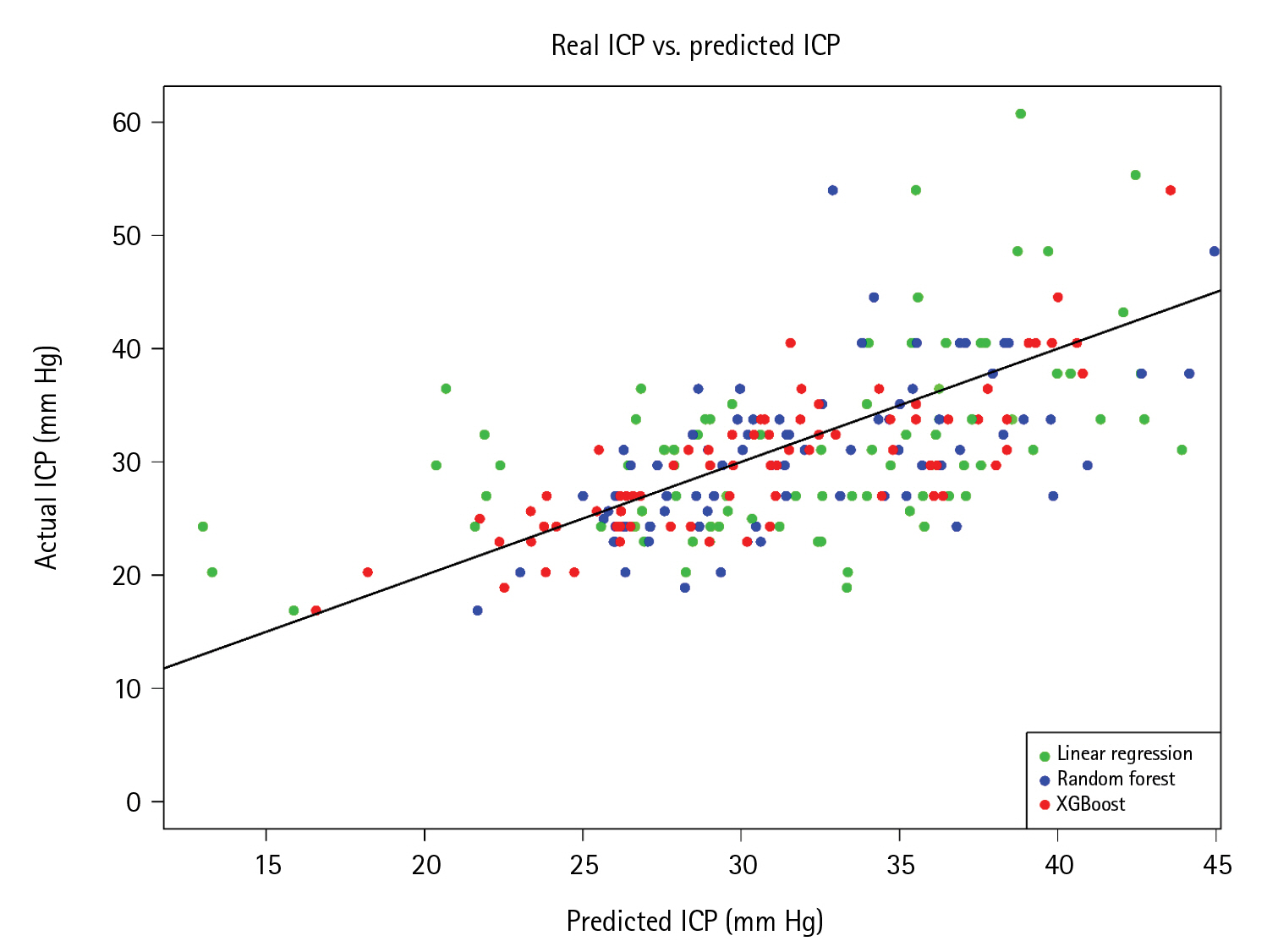
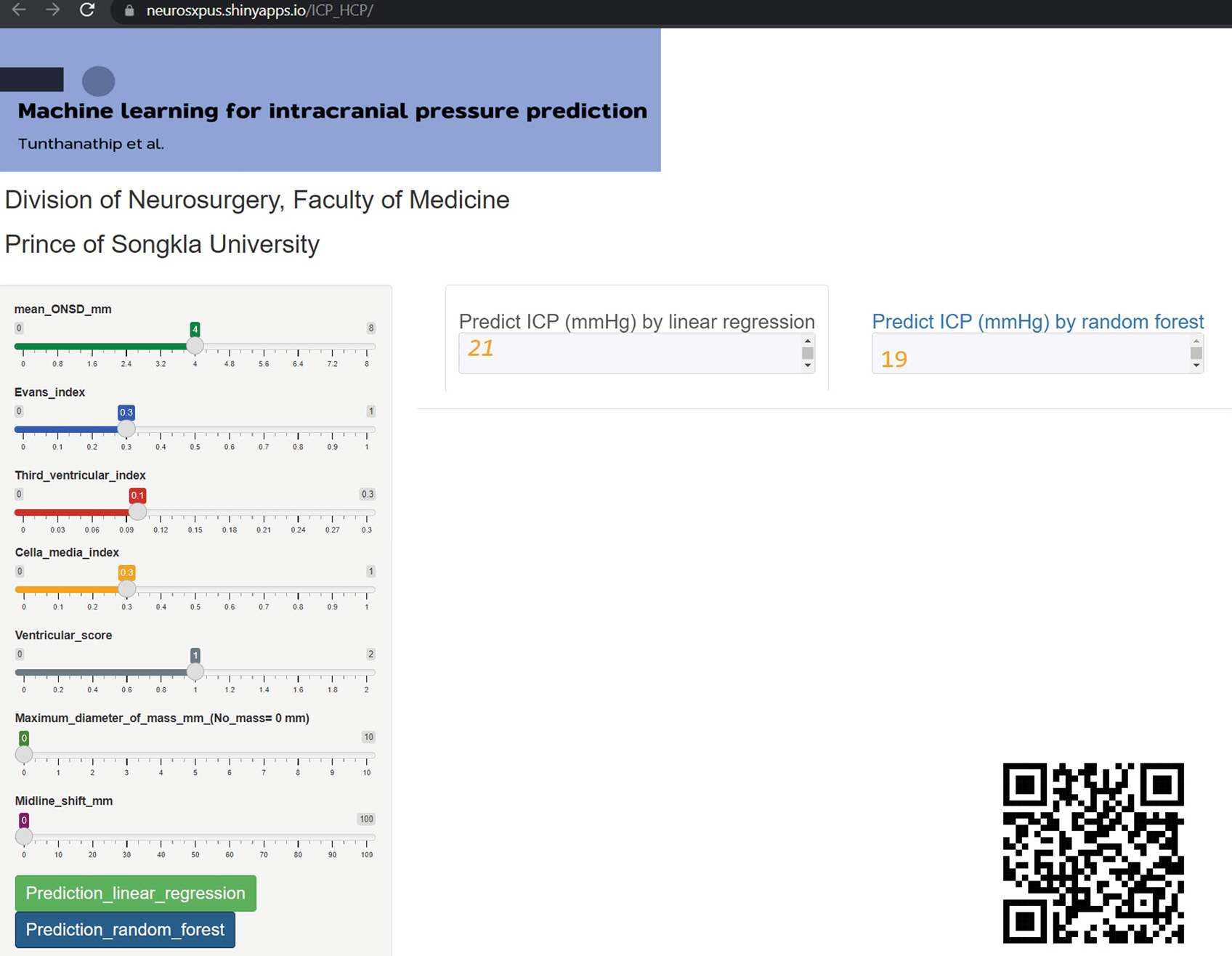
The cubic spline regression had the lowest MAE and RMSE in the first strategy of model development. However, low R2 values in all regression models were observed and ranged from 0.10–0.17. In the second strategy, the addition of ventricular indexes in the model increased R2 dramatically to 0.34 and 0.50 in RF and XGBoost algorithms, respectively. Moreover, the XGBoost regression had the lowest errors among the models. Model development with the third strategy revealed slightly increased predictive performances, with RF and XGBoost algorithms still exhibiting low errors and high R2 values. Compared to linear regression, Figure 4 shows the real and predicted ICP values calculated by RF and XGBoost algorithms. The ICP that was predicted by XGBoost was closer to the regression line than those of linear and RF regression. For general-practice implications, we enable access to the web application at https://neurosxpus.shinyapps.io/ICP_HCP/, as shown in Figure 5.
DISCUSSION
In previous studies, the relationships between ONSD and ventricular indexes to ICP have remained unclear [6-8]. Here, we found that ONSD was significantly correlated with ICP using linear correlation. The concordance results in this study were like those reported by previous studies [5,18]. Lee et al. [5] revealed a significantly positive link between ONSD and ICP, with a yield of enhanced ICP categorization by the area under the receiver operating characteristic curve (AUC) of 0.834, whereas Jeon et al. [18] found that ONSD was associated with increased ICP and reported an AUC of 0.936.
While ONSD correlated statistically and significantly with ICP, none of the ventricular markers showed a correlation, consistent with the findings of Kavi et al. [6]. Although there were no statistical connections between ventricular indexes and ICP in the present study, we discovered that these indexes were useful for ICP prediction using ensemble learning. When ventricular indexes were included in the second strategy of model development, the R2 value, which reflects the percentage of explanation by independent variables, increased. According to logical explanation, ventricular indexes represent the severity of the ventricular size that should directly affect ICP [14].
Both the XGBoost and the RF ensemble learning algorithms had low MAE and RMSE values for ICP prediction. Datasets with vital features provide additional information through meaningful modeling and enhanced performance of the prediction [19]. In addition, XGBoost and RF algorithms had high predictive performances.
The XGBoost algorithm has been used extensively for predicting clinical outcomes in neurosurgery, including in glioma [20], traumatic brain injury [21], spinal cord injury [22], and subarachnoid hemorrhage [23]. However, research that discusses the predictive performance of continuous variable outcomes is lacking. While RF regression was used to predict continuous variable outcomes from the literature review, Tunthanathip et al. [24] reported RF regression that was effective and precise enough to predict the number of units of blood product necessary for a brain tumor operation. Moreover, ML could optimize the over-requesting of preoperative blood products and reduce preoperative costs by 47.88%–67.88% [24].
Although the XGBoost and RF algorithms allow fewer errors than linear regression for ICP prediction, clinicians in general practice may be comfortable with the simplicity of linear regression. As a result, the user-friendliness of a tool is one of the most important criteria linked to physician utilization in the real world. We developed an ML-based online application that only requires predictor variables to be entered, after which cloud ML models will output the expected ICPs. This deployment is in concordance with other research reports [24,25].
To the best of our knowledge, the present study was the first to use various ML regression models to predict ICP in patients with HCP. Therefore, ML may be an alternative non-invasive procedure for application in patients who have contraindications, such as unstable vital signs or coagulopathy. However, the limitations of the present study should be noted. There have been several techniques of ONSD measurement used in prior studies, such as ultrasonography [18] and cranial CT imaging [5-7]. An axial view of a cranial CT scan is one of the acceptable methods, whereas ONSD measurement by ultrasonography may be limited by operator dependence [7]. To validate generalizability, the ML model needs to be estimated using additional data for improvement of predictive performance [26,27].
Ensemble learning techniques, including XGBoost and RF algorithms, are useful for estimating preoperative ICP and prognosticating HCP in patients. Furthermore, ML-based prediction may be an effective non-invasive approach to use in future challenges.
KEY MESSAGES
▪ Hydrocephalus is a major issue for neurosurgical patients that can result in death and disability.
▪ Machine learning is currently being used to predict a variety of therapeutic outcomes in different neurosurgical domains.
▪ Machine learning algorithms are helpful for predicting intracranial pressure in patients with hydrocephalus.
NOTES
-
CONFLICT OF INTEREST
No potential conflict of interest relevant to this article was reported.
-
FUNDING
None.
-
AUTHOR CONTRIBUTIONS
Conceptualization: TT. Methodology: TT. Formal analysis: TT. Data curation: AT. Visualization: TT. Project administration: TT. Funding acquisition: TT. Writing–original draft: all authors. Writing–review & editing: TT.
Acknowledgments
None.
Figure 1.Patient flowchart for inclusion and analysis.

Figure 2.Measurement of ventricular parameters and optic nerve sheath diameters. (A) Ventricular parameters at the level of the foramen of Monro. (B) Ventricular parameters at the level of the cella media. (C) Optic nerve sheath diameter measurement.
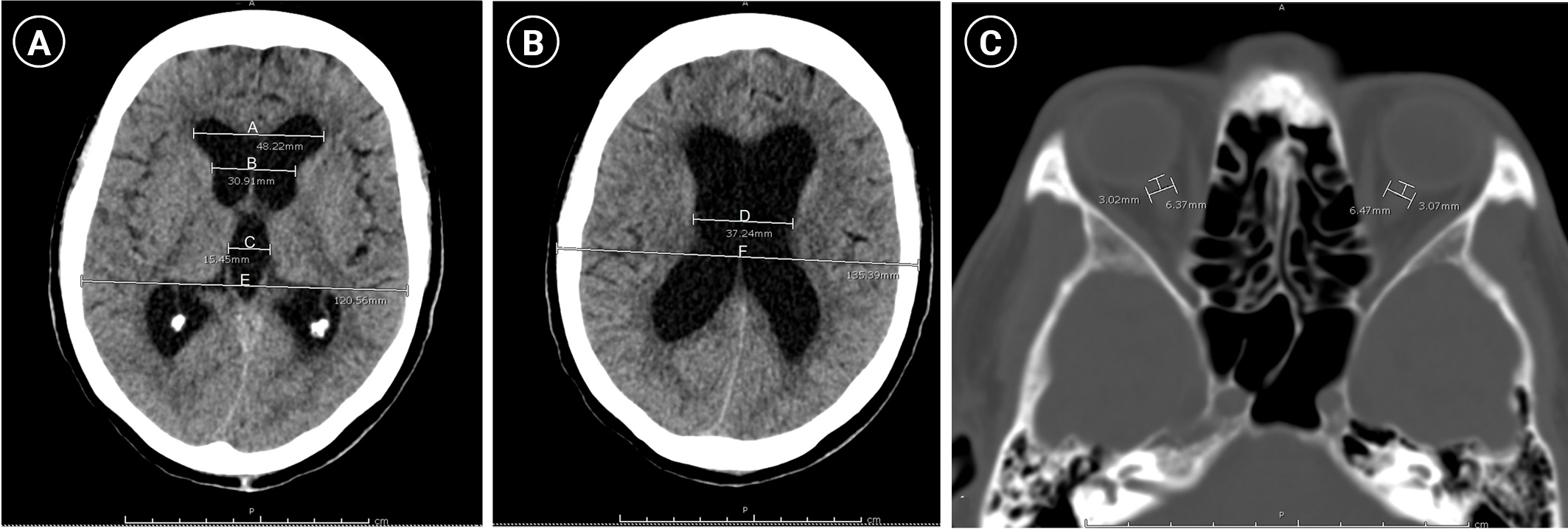
Figure 3.Correlation matrix of various parameters together with their scatterplots. ONSD: optic nerve sheath diameter; A: the maximum bifrontal distance of the lateral ventricle; B: the distance between the caudate nuclei at the level of the foramen of Monro; C: the maximum width of the third ventricle; D: the minimum width of both cella media; E: the maximum inner diameter of the skull at the level of the maximum bifrontal distance measurement; F: the maximal outer interparietal diameter; Ventri: ventricular score; Mass: mass diameter; MLS: midline shift; ICP: intracranial pressure.
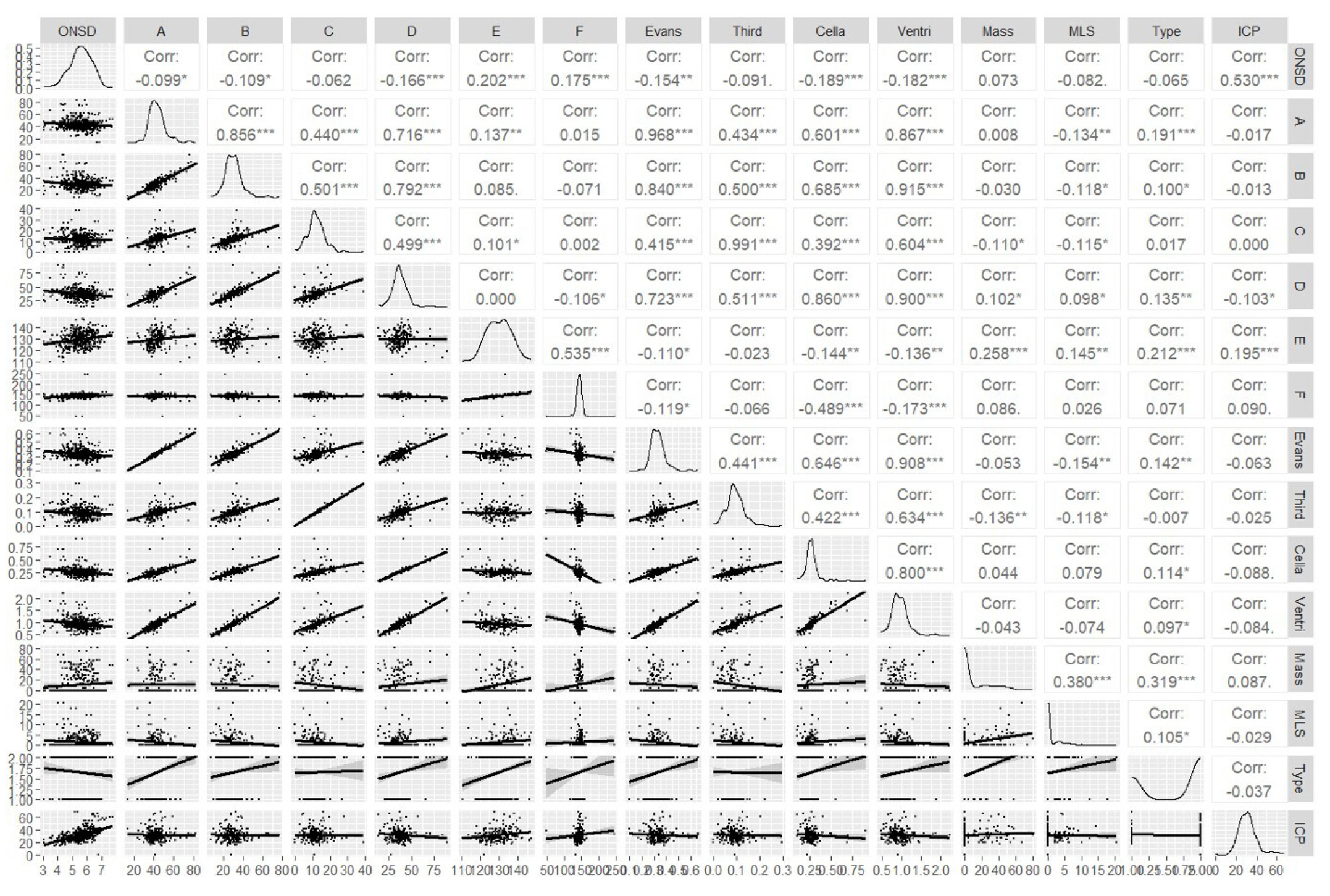
Figure 4.Scatterplots of actual and predicted intracranial pressure (ICP) among linear regression, random forest, and extreme gradient boosting (XGBoost) using test data with the third model.
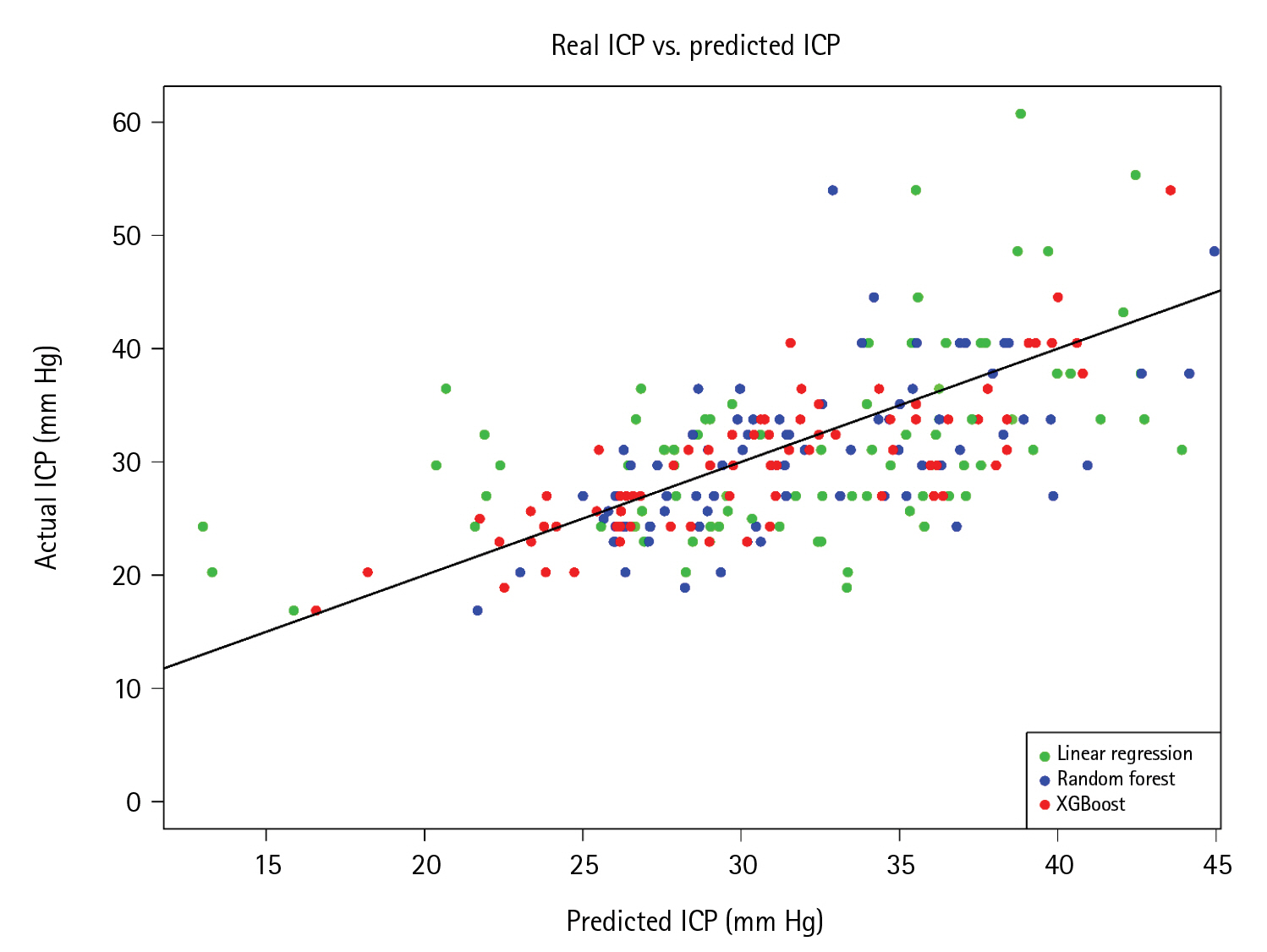
Figure 5.A screen capture of the sample web application for predicting intracranial pressure (ICP). ONSD: optic nerve sheath diameter.
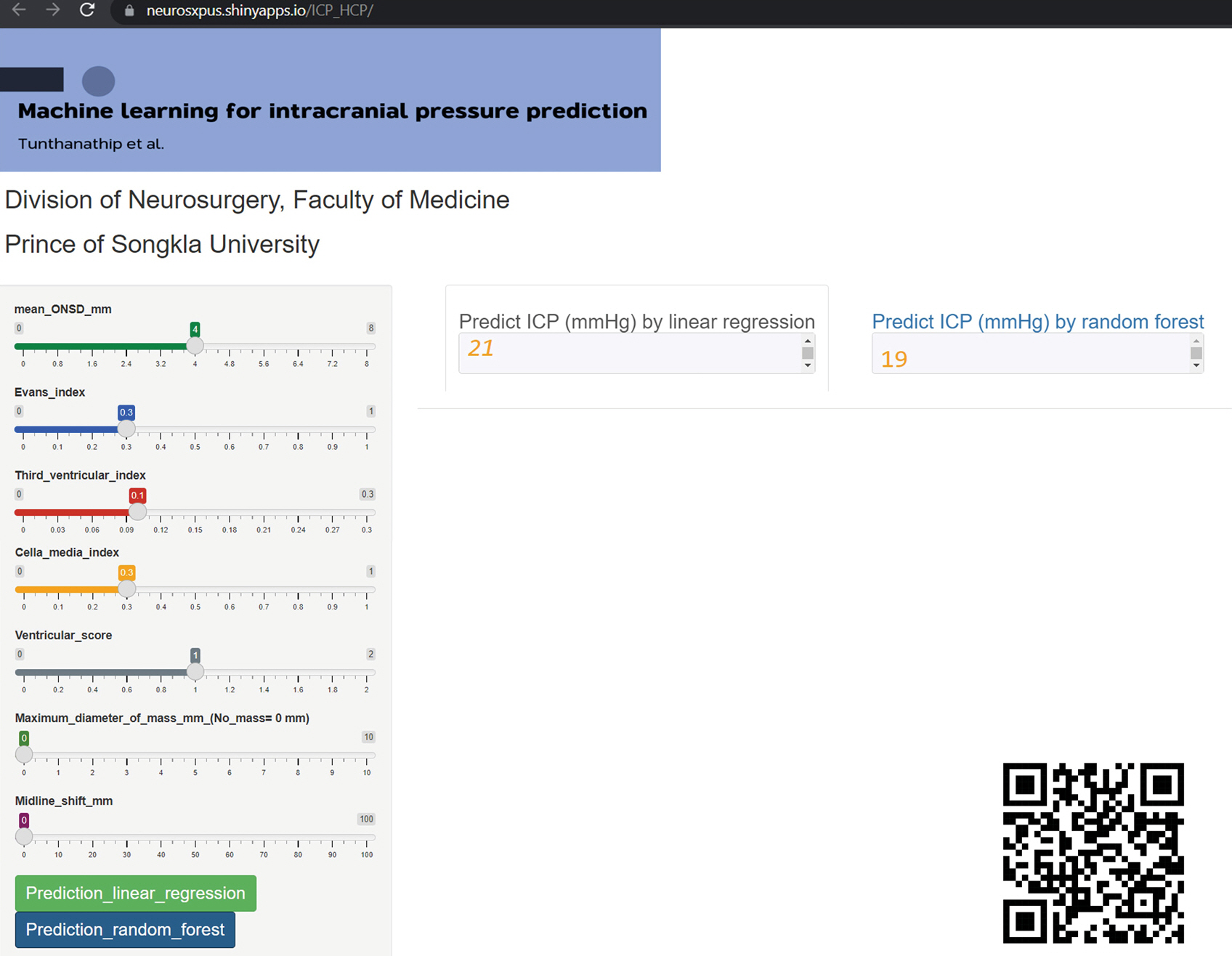
Table 1.Baseline characteristics of the present cohort
|
Characteristics |
Value (n=412) |
|
Sex |
|
|
Male |
196 (47.6) |
|
Female |
216 (52.4) |
|
Age (yr) |
51±24 |
|
Underlying disease |
|
|
Hypertension |
120 (29.1) |
|
Diabetes |
46 (11.2) |
|
Dyslipidemia |
40 (9.7) |
|
Renal failure |
23 (5.8) |
|
Liver disease |
6 (1.5) |
|
American Association of Anesthesiologists classification |
|
|
2 |
8 (1.9) |
|
3 |
320 (77.7) |
|
4 |
80 (19.4) |
|
Signs and symptoms |
|
|
Headache |
132 (32.0) |
|
Motor weakness |
310 (75.2) |
|
Ataxia |
12 (2.9) |
|
Preoperative seizure |
38 (9.2) |
|
Preoperative Glasgow coma scale score |
|
|
13–15 |
66 (16.0) |
|
9–12 |
102 (24.8) |
|
3–8 |
244 (59.2) |
|
Pupillary light reflex |
|
|
Fixed both eyes |
56 (13.6) |
|
React one eye |
32 (7.8) |
|
React both eyes |
324 (78.6) |
|
Type of hydrocephalus |
|
|
Communicating hydrocephalus |
146 (35.4) |
|
Obstructive hydrocephalus |
266 (64.6) |
|
Basal cistern obliteration |
194 (47.1) |
|
Emergency operation |
388 (94.2) |
|
Mean intracranial pressure (mm Hg) |
31.4±9.5 |
Table 2.Average imaging parameters and indexes
|
Parameter/index |
Mean±SD |
|
Optic nerve sheet diameter (mm) |
5.5±0.8 |
|
A (mm) |
43.2±9.4 |
|
B (mm) |
30.5±9.5 |
|
C (mm) |
12.1±5.2 |
|
D (mm) |
37.8±10.2 |
|
E (mm) |
129.9±6.5 |
|
F (mm) |
142.7±12.2 |
|
Evans index (A/E) |
0.3±0.1 |
|
Third ventricular index (C/E) |
0.1±0.0 |
|
Cella media index (D/F) |
0.3±0.1 |
|
Ventricular score ([A+B+C+D/E]×100) |
95.3±23.7 |
|
Midline shift (mm) |
1.5±3.1 |
|
Mass diameter (mm) |
11.1±18.6 |
Table 3.Predictive performances of various models for intracranial pressure
|
Model |
MAE |
RMSE |
R2
|
|
1st model (ONSD) |
|
Linear regression |
6.45 |
8.59 |
0.15 |
|
Polynomial regression |
6.27 |
8.56 |
0.16 |
|
Log transformation |
6.47 |
8.60 |
0.14 |
|
Cubic spline regression |
6.26 |
8.54 |
0.16 |
|
KNN (k=9) |
6.55 |
8.95 |
0.11 |
|
DT |
6.62 |
8.95 |
0.10 |
|
RF |
7.10 |
9.70 |
0.14 |
|
XGBoost |
6.34 |
8.70 |
0.17 |
|
ANN |
6.30 |
8.58 |
0.16 |
|
2nd model (ONSD with ventricular indexesa)) |
|
Linear regression |
6.43 |
8.59 |
0.15 |
|
Polynomial regression |
6.03 |
8.23 |
0.17 |
|
Log transformation |
6.23 |
8.41 |
0.14 |
|
Cubic spline regression |
6.01 |
8.15 |
0.17 |
|
KNN (k=5) |
6.07 |
8.48 |
0.13 |
|
DT |
6.75 |
9.04 |
0.13 |
|
RF |
5.02 |
7.42 |
0.34 |
|
XGBoost |
3.89 |
6.46 |
0.50 |
|
ANN |
6.48 |
8.88 |
0.16 |
|
3rd model (ONSD+ventricular indexesa)+other parametersb)) |
|
Linear regression |
6.70 |
8.73 |
0.16 |
|
Polynomial regression |
6.50 |
8.91 |
0.08 |
|
Log transformation |
6.49 |
8.88 |
0.01 |
|
Cubic spline regression |
6.75 |
9.08 |
0.01 |
|
KNN (k=5) |
5.75 |
8.15 |
0.18 |
|
DT |
6.06 |
8.24 |
0.22 |
|
RF |
4.67 |
6.98 |
0.41 |
|
XGBoost |
3.62 |
6.72 |
0.51 |
|
ANN |
6.48 |
8.88 |
0.16 |
References
- 1. Barthélemy EJ, Park KB, Johnson W. Neurosurgery and sustainable development goals. World Neurosurg 2018;120:143-52.ArticlePubMed
- 2. Sinclair JR. Importance of a one health approach in advancing global health security and the sustainable development goals. Rev Sci Tech 2019;38:145-54.PubMed
- 3. Vinchon M, Rekate H, Kulkarni AV. Pediatric hydrocephalus outcomes: a review. Fluids Barriers CNS 2012;9:18. ArticlePubMedPMCPDF
- 4. Treggiari MM, Schutz N, Yanez ND, Romand JA. Role of intracranial pressure values and patterns in predicting outcome in traumatic brain injury: a systematic review. Neurocrit Care 2007;6:104-12.ArticlePubMedPDF
- 5. Lee HC, Lee WJ, Dho YS, Cho WS, Kim YH, Park HP. Optic nerve sheath diameter based on preoperative brain computed tomography and intracranial pressure are positively correlated in adults with hydrocephalus. Clin Neurol Neurosurg 2018;167:31-5.ArticlePubMed
- 6. Kavi T, Gupta A, Hunter K, Schreiber C, Shaikh H, Turtz AR. Optic nerve sheath diameter assessment in patients with intracranial pressure monitoring. Cureus 2018;10:e3546.ArticlePubMedPMC
- 7. Jenjitranant P, Tunlayadechanont P, Prachanukool T, Kaewlai R. Correlation between optic nerve sheath diameter measured on imaging with acute pathologies found on computed tomography of trauma patients. Eur J Radiol 2020;125:108875. ArticlePubMed
- 8. Kim E, Lim YJ, Park HS, Kim SK, Jeon YT, Hwang JW, et al. The lack of relationship between intracranial pressure and cerebral ventricle indices based on brain computed tomography in patients undergoing ventriculoperitoneal shunt. Acta Neurochir (Wien) 2015;157:257-63.ArticlePubMedPDF
- 9. Eide PK. The relationship between intracranial pressure and size of cerebral ventricles assessed by computed tomography. Acta Neurochir (Wien) 2003;145:171-9.ArticlePubMedPDF
- 10. Tunthanathip T, Sae-Heng S, Oearsakul T, Sakarunchai I, Kaewborisutsakul A, Taweesomboonyat C. Machine learning applications for the prediction of surgical site infection in neurological operations. Neurosurg Focus 2019;47:E7. Article
- 11. Miyagawa T, Sasaki M, Yamaura A. Intracranial pressure based decision making: prediction of suspected increased intracranial pressure with machine learning. PLoS One 2020;15:e0240845.ArticlePubMedPMC
- 12. Schweingruber N, Mader MM, Wiehe A, Röder F, Göttsche J, Kluge S, et al. A recurrent machine learning model predicts intracranial hypertension in neurointensive care patients. Brain 2022;145:2910-9.ArticlePubMedPMCPDF
- 13. Hainke T. Centimeter of water column into millimeter of water column [Internet]. Convert-measurement-units.com; 2022 [cited 2023 Jun 19]. Available from: https://www.convert-measurement-units.com/convert+Centimeter+of+water%20+column+to+Millimeter+of+mercury.php.
- 14. Mataró M, Poca MA, Sahuquillo J, Cuxart A, Iborra J, de la Calzada MD, et al. Cognitive changes after cerebrospinal fluid shunting in young adults with spina bifida and assumed arrested hydrocephalus. J Neurol Neurosurg Psychiatry 2000;68:615-21.ArticlePubMedPMC
- 15. The BMJ. Correlation and regression [Internet]. The BMJ. 2022;[cited 2023 Jun 19]. Available from: https://www.bmj.com/about-bmj/resources-readers/publications/statistics-square-one/11-correlation-and-regression.
- 16. Truc TT. Statistics and sample size pro [Internet]. Google LLC; 2020;[cited 2023 Jun 19]. Available from: https://play.google.com/store/apps/details?id=thaithanhtruc.info.sass&hl=en_US.
- 17. Kassambara A. Machine learning essentials: practical guide in R [Internet]. STHDA. 2017;[cited 2023 Jun 19]. Available from: https://www.datanovia.com/en/wp-content/uploads/dn-tutorials/book-preview/machine-learning-essentials_preview.pdf.
- 18. Jeon JP, Lee SU, Kim SE, Kang SH, Yang JS, Choi HJ, et al. Correlation of optic nerve sheath diameter with directly measured intracranial pressure in Korean adults using bedside ultrasonography. PLoS One 2017;12:e0183170.ArticlePubMedPMC
- 19. Goldrick S, Sandner V, Cheeks M, Turner R, Farid SS, McCreath G, et al. Multivariate data analysis methodology to solve data challenges related to scale-up model validation and missing data on a micro-bioreactor system. Biotechnol J 2020;15:e1800684.ArticlePubMedPDF
- 20. Yan Z, Wang J, Dong Q, Zhu L, Lin W, Jiang X. XGBoost algorithm and logistic regression to predict the postoperative 5-year outcome in patients with glioma. Ann Transl Med 2022;10:860. ArticlePubMedPMC
- 21. Wang R, Wang L, Zhang J, He M, Xu J. XGBoost machine learning algorism performed better than regression models in predicting mortality of moderate-to-severe traumatic brain injury. World Neurosurg 2022;163:e617-22.ArticlePubMed
- 22. Inoue T, Ichikawa D, Ueno T, Cheong M, Inoue T, Whetstone WD, et al. XGBoost, a machine learning method, predicts neurological recovery in patients with cervical spinal cord injury. Neurotrauma Rep 2020;1:8-16.ArticlePubMedPMC
- 23. Wang R, Zhang J, Shan B, He M, Xu J. XGBoost machine learning algorithm for prediction of outcome in aneurysmal subarachnoid hemorrhage. Neuropsychiatr Dis Treat 2022;18:659-67.ArticlePubMedPMCPDF
- 24. Tunthanathip T, Sae-Heng S, Oearsakul T, Kaewborisutsakul A, Taweesomboonyat C. Economic impact of a machine learning-based strategy for preparation of blood products in brain tumor surgery. PLoS One 2022;17:e0270916.ArticlePubMedPMC
- 25. Tunthanathip T, Duangsuwan J, Wattanakitrungroj N, Tongman S, Phuenpathom N. Comparison of intracranial injury predictability between machine learning algorithms and the nomogram in pediatric traumatic brain injury. Neurosurg Focus 2021;51:E7. Article
- 26. Taweesomboonyat C, Kaewborisutsakul A, Tunthanathip T, Saeheng S, Oearsakul T. Necessity of in-hospital neurological observation for mild traumatic brain injury patients with negative computed tomography brain scans. J Health Sci Med Res 2020;38:267-74.ArticlePDF
- 27. Tunthanathip T, Duangsuwan J, Wattanakitrungroj N, Tongman S, Phuenpathom N. Clinical nomogram predicting intracranial injury in pediatric traumatic brain injury. J Pediatr Neurosci 2020;15:409-15.ArticlePubMed
Citations
Citations to this article as recorded by

 , Thara Tunthanathip
, Thara Tunthanathip







 KSCCM
KSCCM

 PubReader
PubReader ePub Link
ePub Link Cite
Cite